GÉOMÉTRIE DU BALLON DE FOOT
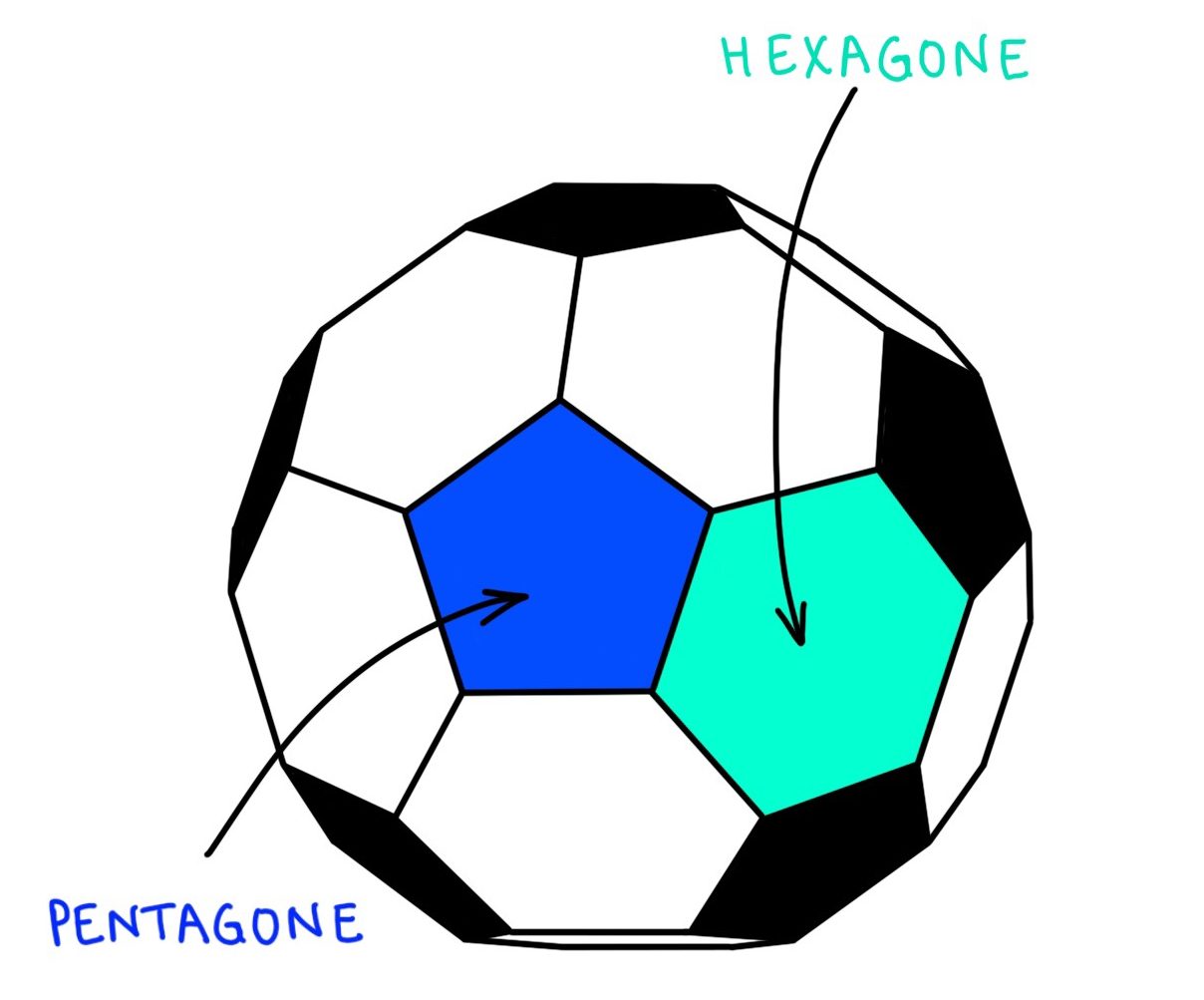
Le ballon de foot a fait l'objet de plusieurs études scientifiques notamment en aérodynamique. La forme et la structure du ballon jouent un rôle important dans la trajectoire et la vitesse de celui-ci. Pour fabriquer un ballon de foot classique, des pièces en forme de polygones sont cousues entre elles pour obtenir une forme sphérique. Pendant longtemps, les ballons de foot étaient composés de 32 pièces : 20 hexagones et 12 pentagones. En mathématiques, on appelle ce solide un icosaèdre tronqué.
À la coupe du monde 2006, le ballon de foot "Teamgeist" ( "esprit d'équipe" en allemand ) a fait parler de lui. Composé uniquement de 14 pièces, il a surpris plus d'un gardien en suivant des trajectoires imprévisibles. Le ballon officiel de la coupe du monde 2014 a été testé dans les tunnels aérodynamiques de la NASA pour éviter les problèmes de trajectoires.
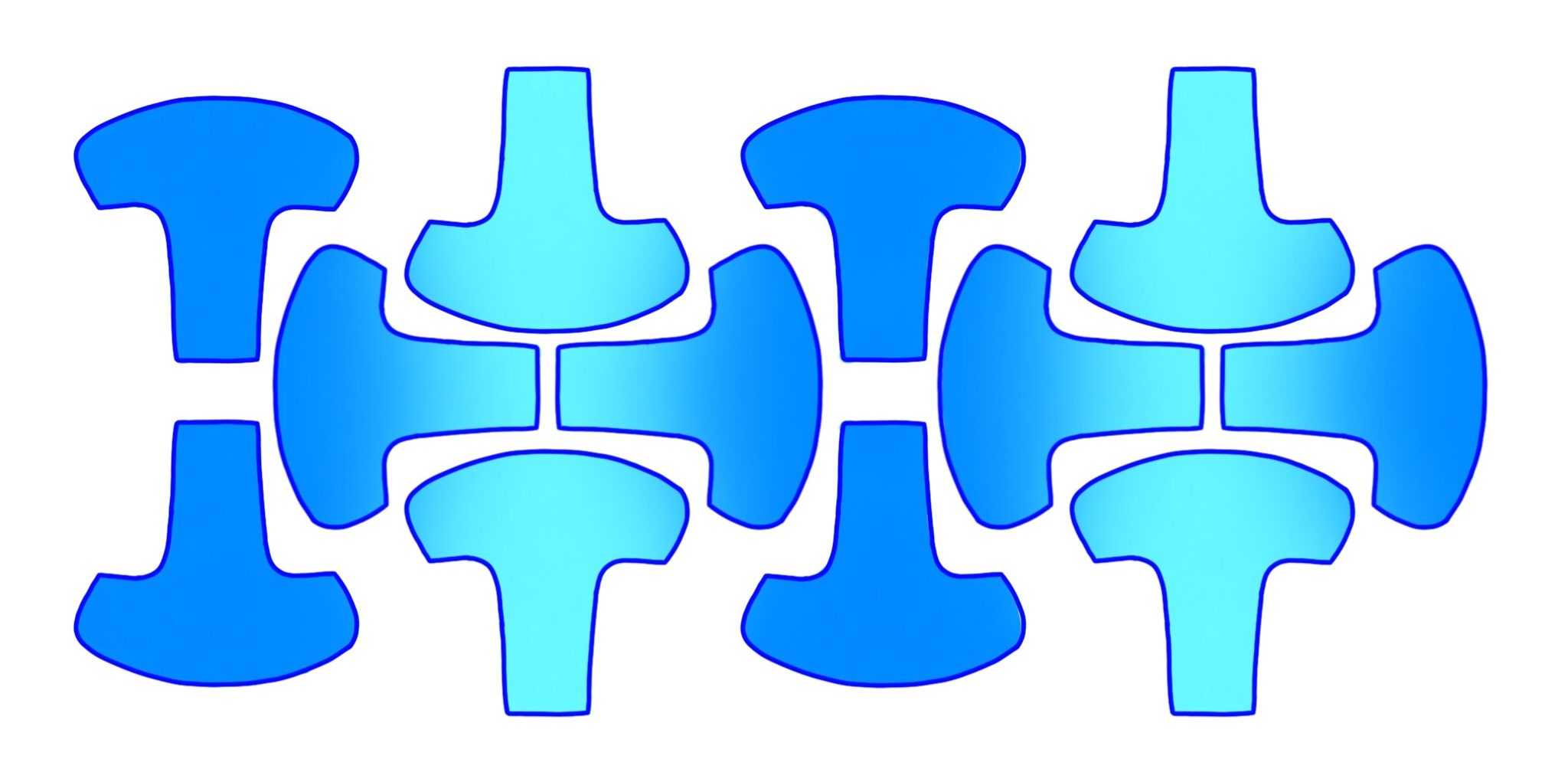
Ce ballon de foot est composé de 6 pièces identiques. Ces pièces possèdent un centre de symétrie mais ne possèdent pas d'axe de symétrie.
Pour la CAN 2017, le ballon est composé de 12 pièces identiques. Ces pièces possèdent un axe de symétrie mais ne possèdent pas de centre de symétrie.
FRAPPE ENROULÉE, EXTÉRIEUR DU PIED
En 1997, lors d'un match amical entre la France et le Brésil, un joueur brésilien du nom de Roberto Carlos, a marqué un but légendaire. Sur un coup de pied arrêté, à 35 mètres du but, il a réussi à mettre le ballon au fond du filet, ce qui semblait pratiquement impossible. Voici un schéma, vu du haut, de la position du coup-franc :
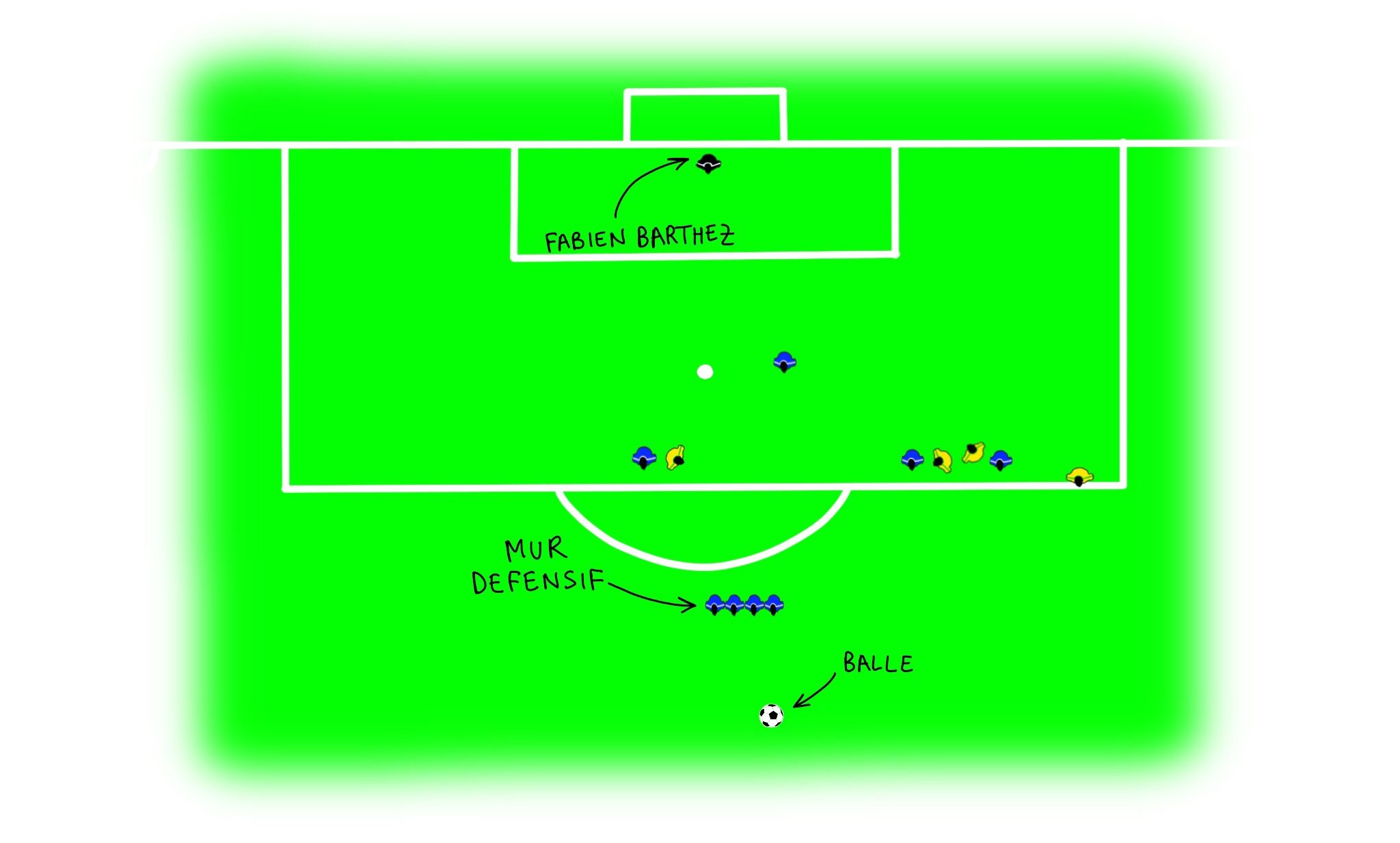
En observant la situation, il ne semble pas y avoir de possibilités, à cause du mur défensif qui bloque tous les tirs rectilignes. Mais alors, comment marquer? Il faut, pour cela, étudier un phénomène physique connu sous le nom de l'effet Magnus.
D'après la première loi de Newton, une balle qui se déplace garde la même direction et la même vitesse à moins qu'une force vienne modifier ces deux facteurs. Quelles sont les forces qui s'exercent sur un ballon?
- La force de gravité va faire tomber la balle, mais elle ne va pas la faire dévier à gauche ou à droite.
- L'air crée aussi une force (force de frottement) qui va ralentir la balle, mais là encore, cela ne va pas modifier sa trajectoire rectiligne.
En regardant de plus près la frappe, extérieur du pied, de Roberto Carlos, on s'aperçoit qu'il fait tourner le ballon sur lui-même. En pivotant sur lui-même durant son déplacement, le ballon crée une nouvelle force, la force Magnus. Comment ça marche?
La vitesse de l'air, d'un côté du ballon, va augmenter , ce qui va faire diminuer la pression de l'air. De l'autre côté du ballon, la vitesse de l'air diminue ce qui fait augmenter la pression. Cette différence de pression va faire dévier le ballon vers la gauche comme le montre le schéma ci-dessous :
Voilà donc le moyen de tirer ce coup-franc:
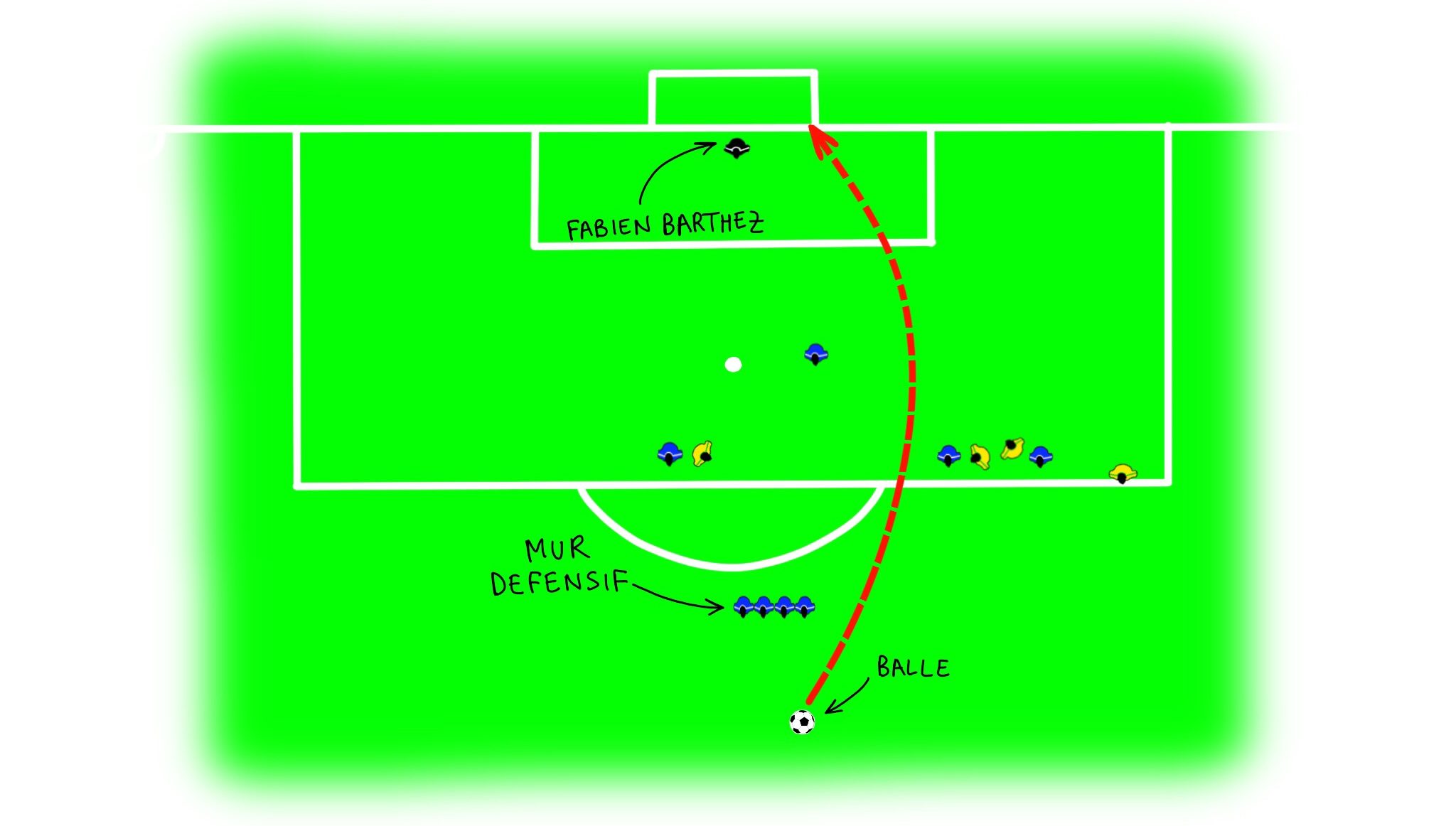
Cette trajectoire est très difficile à obtenir et demande beaucoup d'entrainement mais aussi une bonne compréhension du phénomène. Des étudiants de l'université de Leicester ont trouvé une formule mathématique qui permet de mieux tirer les pénalités et les coup-francs. Cette formule donne l'écart qu'il y'a, à la fin, entre la trajectoire rectiligne et la trajectoire enroulée. Par exemple, si un joueur, situé à 15 mètres du but, tire une balle à une vitesse de 35 mètres par seconde tournant sur elle-même à une vitesse angulaire de 10 révolutions par seconde (sens anti-horaire), la balle aurait alors une déviation de 5 mètres vers la gauche. Voici la formule :
